Introduction

1. Basic half wave rectifier and single smoothing capacitor
2. Basic half wave rectifier and two stage smoothing
3. Full wave rectifier and two stage smoothing

Figure 1 - Basic Capacitor dropper Schematic

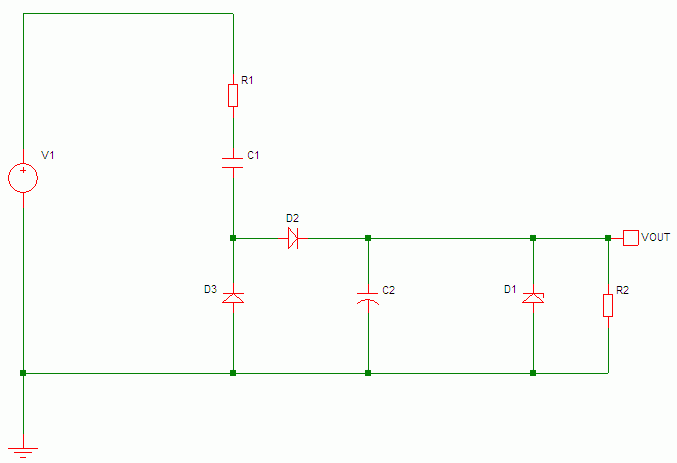
Where;
V1 = AC voltage source
R1 = Peak current limiting resistor
C1 = Dropper capacitor
D2 = Half wave rectifier diode
D3 = Capacitor discharge diode
C2 = DC smoothing capacitor
D1 = DC voltage limiting zener diode
R2 = Resistive load (for simulation purposes)

Initial Design Parameters

To start our capacitor dropper design, we need some initial parameters;

Calculations

1) Input (Supply) current

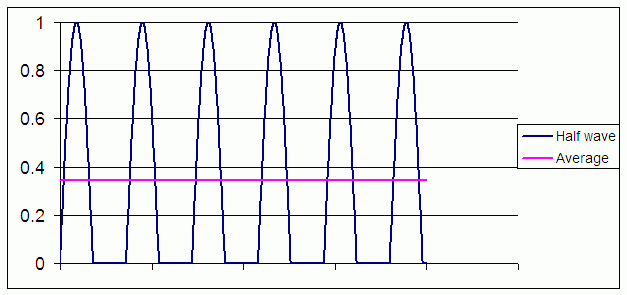
With half wave rectification we are only charging our power supply 50% of the mains cycle, the DC output will be loading the power supply 100% of the time (worst case). Therefore the current draw from the mains during the charge ½ cycle will have to be at least twice the output power.

a) The first step is to calculate our half wave peak current using our DC output current. This is done by multiplying the DC current by 0.344

Figure 2 - Half wave rectified waveform

b) Next, calculate the Iin _RMS value.
As the AC current is full wave (half wave through D2 and the other half through D3) multiply the Iin _PEAK by the root of 2 (or 0.7071)

2) Dropper Capacitor's Reactance

Next we can calculate the reactance required to deliver the desired current at the specified supply voltage.
The voltage drops for the components other than the dropper capacitor are ignored at this time as they are relatively small in comparison.

Where;
Xc = Capacitors reactance in ohms
Vin = Supply voltage
Iin = Input current

Desired reactance = 5837 Ohms

3) Dropper Capacitor's Capacitance

Now we know what reactance we require, we can calculate the capacitor's capacitance

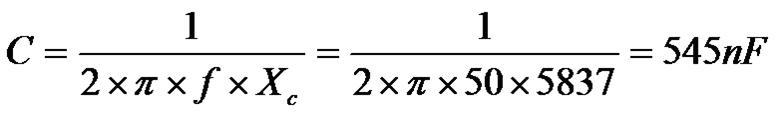
Where;
C = Capacitance
f = Supply frequency
PI = 3.1412
Xc = Capacitors reactance in ohms

The calculated capacitance = 545nF

The nearest preferred value of capacitance is 560nF (being larger will ensure we still meet our 20mA demand)
Next we should recalculate the input current using the preferred value capacitance.

4) New Reactance value

Calculate the reactance using the preferred value

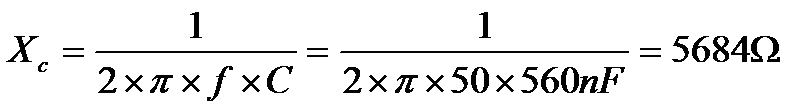
The new reactance value is 5684 Ohms

5) New Input Current

The new input current is now calculated

The new input current is 42.2mA

6) Current Limiting Resistor (R1)

Resistor R1 provides surge current limiting.
When C1 is fully discharged it is an effective zero ohm impedance. When power is first applied particularly is the power is at its peak) the only impedance in the current path is that of the resistor and rectifier diodes
We can now calculate a value for R1

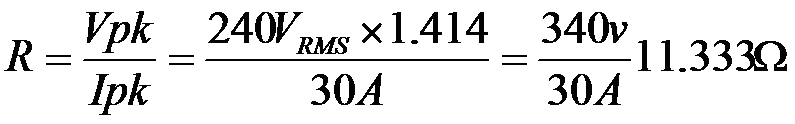
Where;
peak = Mains supply peak voltage
peak = Rectifier diodes non-repetitive peak current

Resistor R1 value = 11.333

Using the nearest preferred value then;

Resistor R1 value = 12 Ohms

7) Re-confirm the peak inrush current using the preferred value for R1

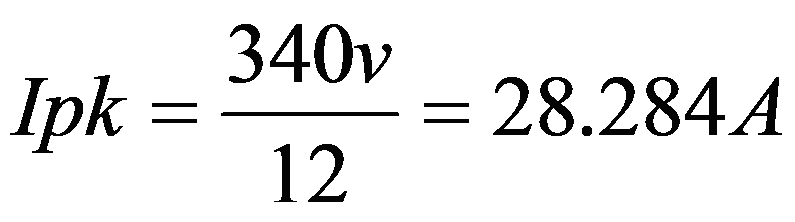
Inrush peak current = 28.3 Amps

8) Average power dissipated by resistor R1

Now we can calculate the power dissipation of R1

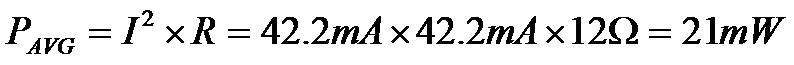
R1 average power = 0.021 Watts = 21mW

9) And the peak power dissipated by resistor R1

R1 peak power = 9600 Watts = 9.6kW

The duration of the peak power can be calculated as follows;

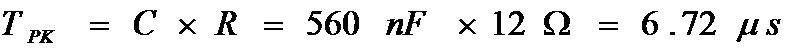
R1 peak power duration = 6.72us

10) Resistor R1 working voltage rating

The resistor working voltage should be greater than the peak mains voltage.

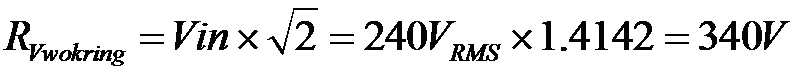
R1 working voltage >= 340V

11) Smoothing Capacitor C2

Capacitor C2 smooths the half wave rectified mains voltage into a steady DC.
The size of capacitor is dependant upon the load current and the acceptable voltage ripple on the DC rail
Assuming that only 8ms of the mains cycle is spent charging the smoothing capacitor (the time when the mains voltage is greater than the capacitor {C2} voltage allowing the rectifier diode {D2} to turn on), then the capacitor will have to supply enough energy to maintain the DC rail for 12ms.

The average current drawn by the DC rail can be calculated as follows;

Where;
I = Average current in amps
C = Capacitance in farads
dv = DC ripple voltage
dt = Time when capacitor supplies the DC rail with current

If we re-arrange this formula we can calculate the capacitance;

Smoothing Capacitor C2 = 0.00048 Farads = 480uF

Using the nearest preferred value then;

Smoothing Capacitor C2 = 560uF

This is quite a large value capacitor and so is 0.5V of ripple. To reduce the ripple by half will mean doubling the capacitor.

Alternatively we can do one of the following;
1. Reduce the output current demand
2. Relax the voltage ripple requirement
3. Implement two stage smoothing / filtering
4. Use full wave rectification

12) Reducing the output load current

We can reduce the size of the smoothing capacitor C2 by reducing the load current.
If we begin by choosing a preferred value for the smoothing capacitor, say 100uF we can the work back to find the load current that will meet our voltage ripple requirement of 0.5V

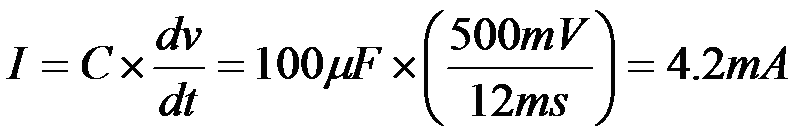
So to use a 100uF capacitor for C2 and keep the ripple voltage to 0.5V our output load current should be reduced to 4.2mA. This is much less than our desired 20mA.
To find the best balance between load current, ripple voltage and smoothing current some iteration and compromise to our requirements is required.

13) Relax our ripple voltage requirement

We can permit a large level of ripple voltage whilst keeping the same load current in order to reduce our smoothing capacitor
So if we set our ripple voltage target to 1volt peak to peak and our load current is kept at 20mA, we can calculate our new capacitor value

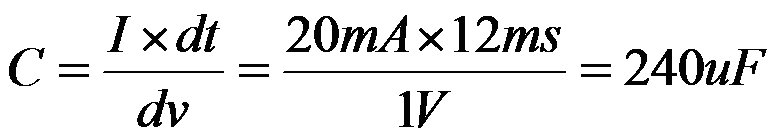
Our smoothing capacitor valve is now 240uF.

This about half our original value but we have twice the ripple voltage.
Again to find the best solution some iteration and compromise of our requirements is needed.

14) Two stage smoothing

This is covered in our Variant 2 design, see Basic half wave rectifier and two stage smoothing in the next section.

15) Full wave rectification

This is covered in our Variant 3 design, see Full wave rectifier and two stage smoothing in the next section.

16) Zener Diode

Zener Voltage
The zener diode voltage should be selected to ensure the output supply voltage is clamped to the maximum permissible voltage above the ideal voltage of our target.

Our target output voltage is 5V

The nearest preferred value of zener voltage above this is 5.1V, the next value is 5.6V.
Our initial selection will be 5.1V as this best matches our target.

Continuous Power Rating

The continuous power rating should be calculated under the condition where the load is pulling its minimum current. So if the load is a resistive load permanently connected the minimum load will be the same as the full load.
But where the load may vary or be switched off the minimum current could be as low as zero amps

Here we shall assume the load can be switched off, therefore the full power supply current will have to be carried by the zener.

a) Find the maximum continuous current supplied by C1

The Maximum output current = 21.1mA

B) Calculate the continuous power dissipation

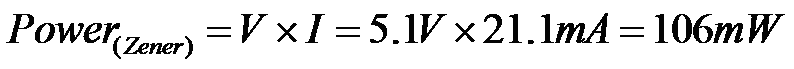
The Zener diode continuous power dissipation = 106mW

C) Peak power dissipation

The peak power through the zener is dependant upon the following;

• The voltage across the zener at the time of peak power
• The current available from C1
• The slope resistance of the zener diode
• The impedance of both capacitors C1 and C2

Calculations Summary

We have now calculated values for all our power supply components.

Take note that these are the ideal values for our requirements, in practice the actual components will not be exact matches. Also we should ensure the components parameters are better / higher rated than the ones calculated to compensate for all tolerances in our design.

Component tolerance analysis will be discussed later on, for now we shall use the calculated values to perform some simulations and evaluate the circuit under dynamic conditions.

Simulations

Before we can simulate our design we should specify a couple more details as follows;

{Updated: 23rd September 2008}